This is a summary on video series “Essence of calculus” which made by youtuber 3blue1brown. “Essence of calculus” are series videoes in order to provide some intutive of calculus.
Chapter 1
The art of doing mathematics is finding that special case that contains all the germs of generality. –David Hilbert
Math has tendency to reward you when you respect its symmetries.
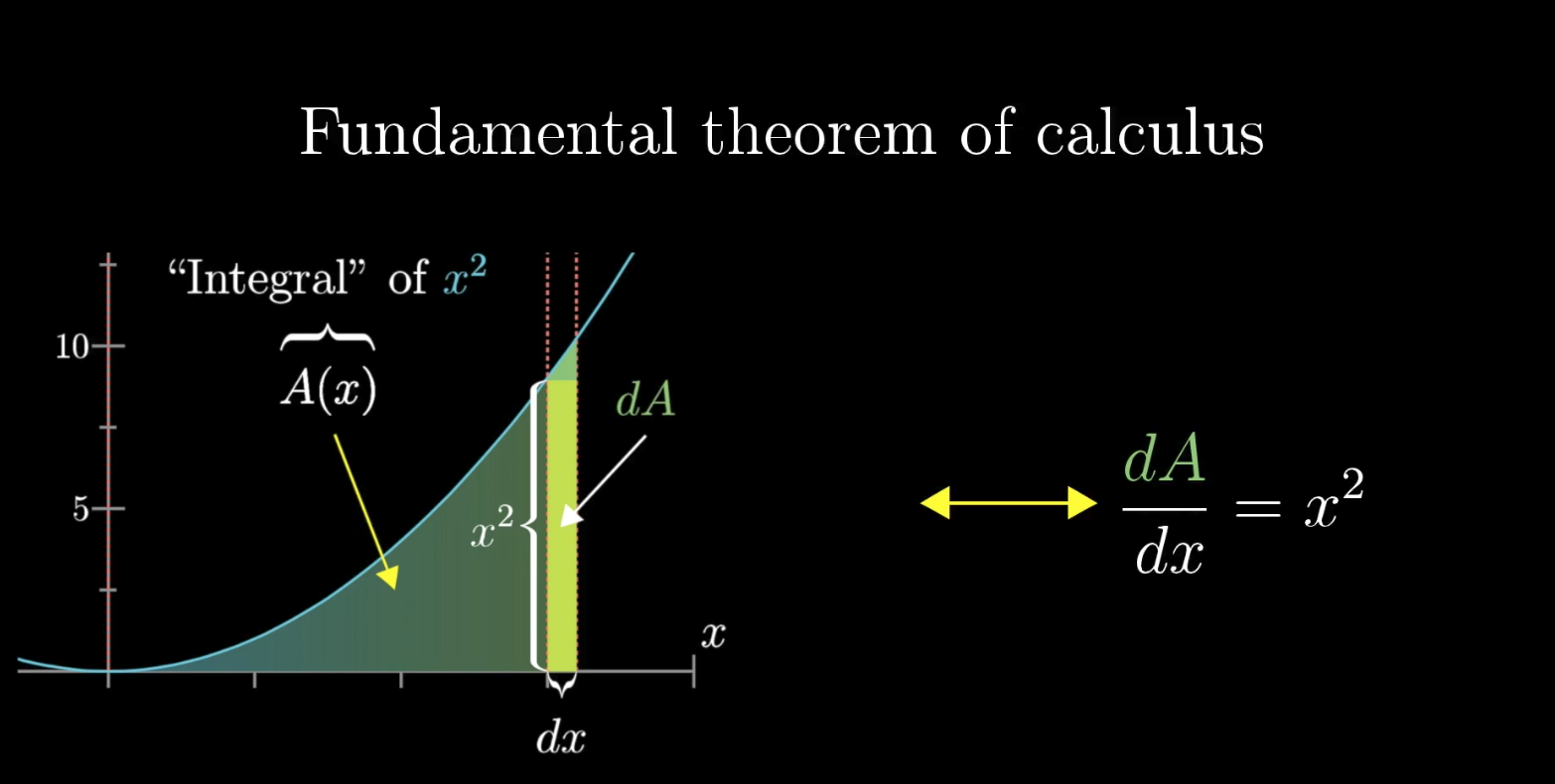
The reason we care about the area under graph is not just for asking hard geometry. It because many practical problem that can be approximated by adding up a large number of small things and can be reframed as a question about an area under a certain graph.
When you come across a genuinely hard question in math, A good policy is not try too hard to get the answer directly but to play around with the idea with no particular goal in mind.
Chapter 2
So far as the theories of mathematics are about reality, they are not certain; So far as they are certain, they are not about reality. –Albert Einstein

dt is neither “infinitely small” nor 0. It is a finitely small, nonzero value which approaching 0 as all.
Derivative is not a instantaneous rate of change but best constant approximation around a point.
Chapter 3
You know, for a mathematician, he did not have enough imagination. But he has become a poet and now he is fine. –David Hilbert
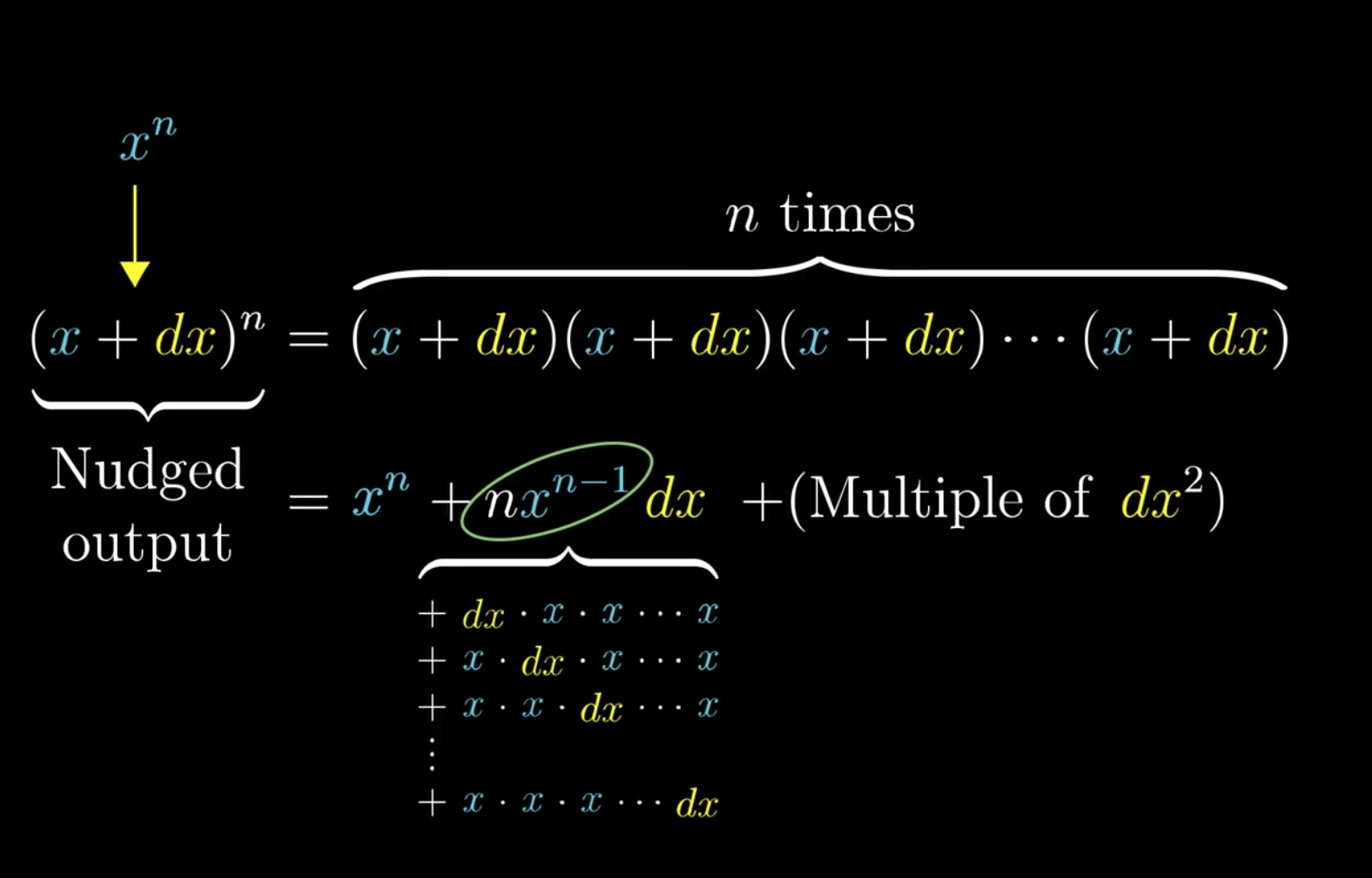
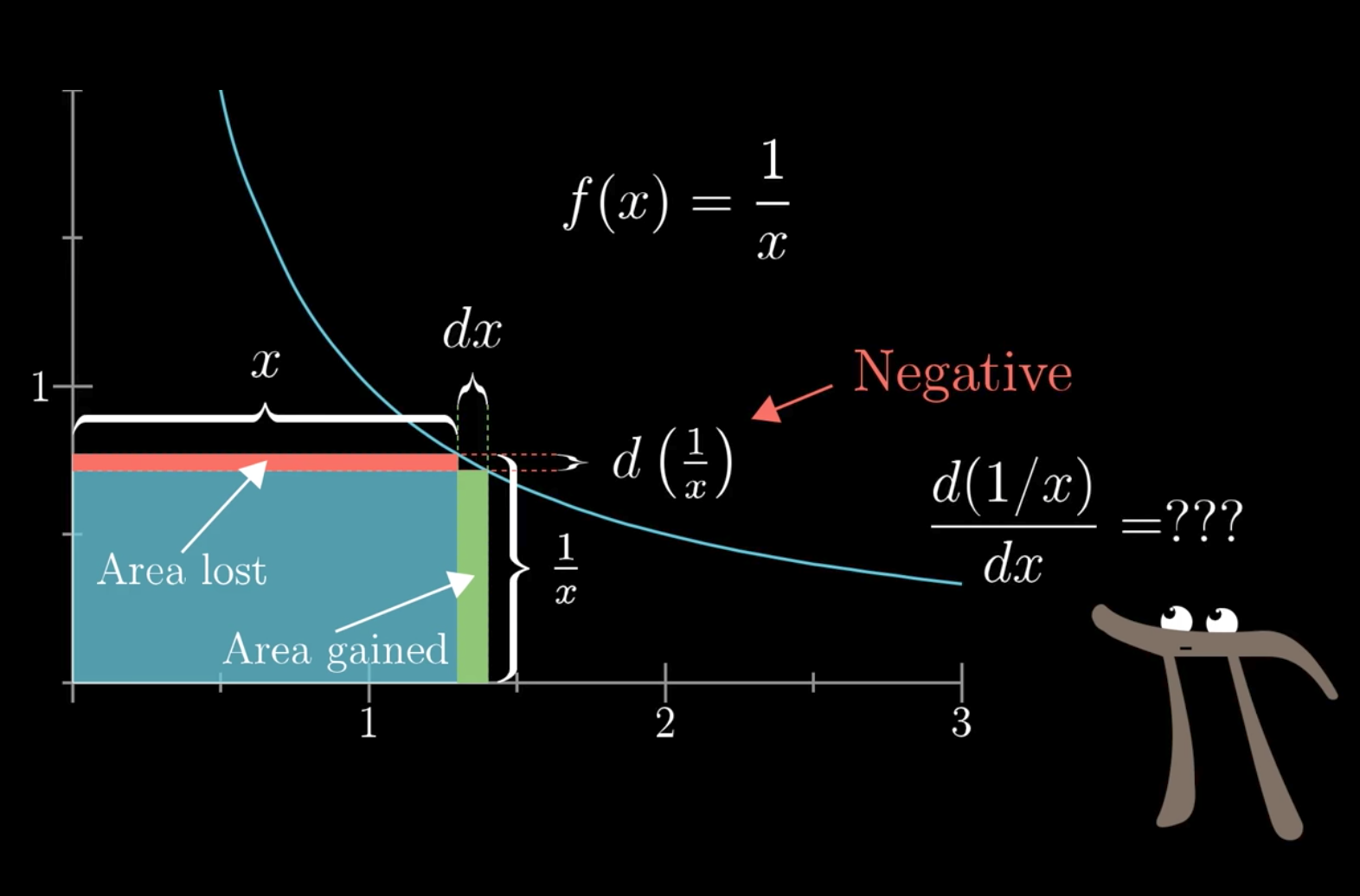
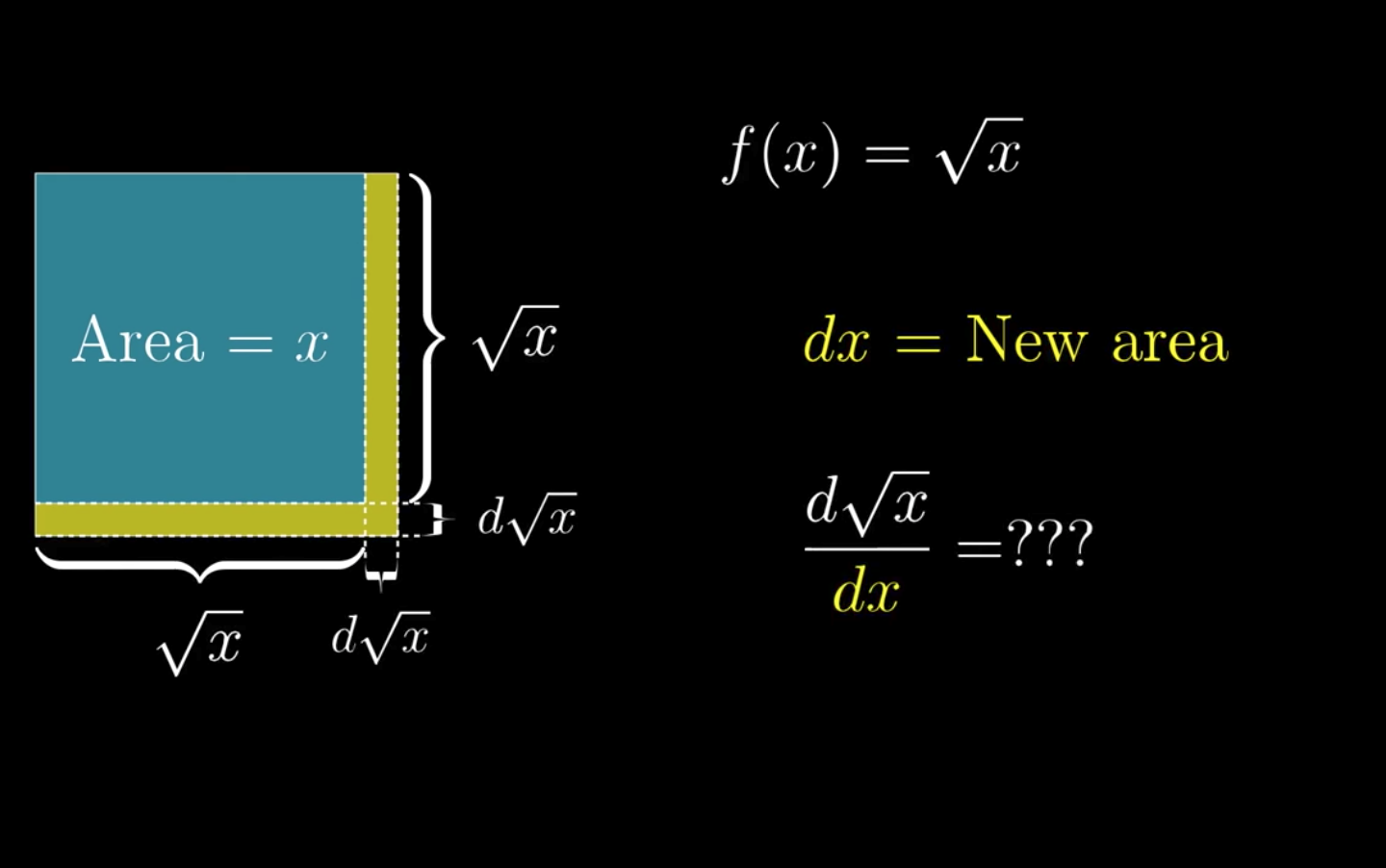
A more exact understanding of the derivative requires looking at what the function actually represents rather than looking at the graph of the function.
Chapter 4
Using the chain rule is like peeling an onion: you have to deal with each layer at a time, and if it is too big you will start to crying. –Anonymous professor

If you are dealing with a product of two things, It is helpful to try to understand it as some form of area.
Chapter 5
Who has not been amazed to learn that the function y = e^x, like a phoenix rising again from its own ashes, is its own derivative? –Francois le Lionnais
a^t = e^ln(a)t
Chapter 6
Do not ask whether a statement is true until you know what it means. –Errett Bishop
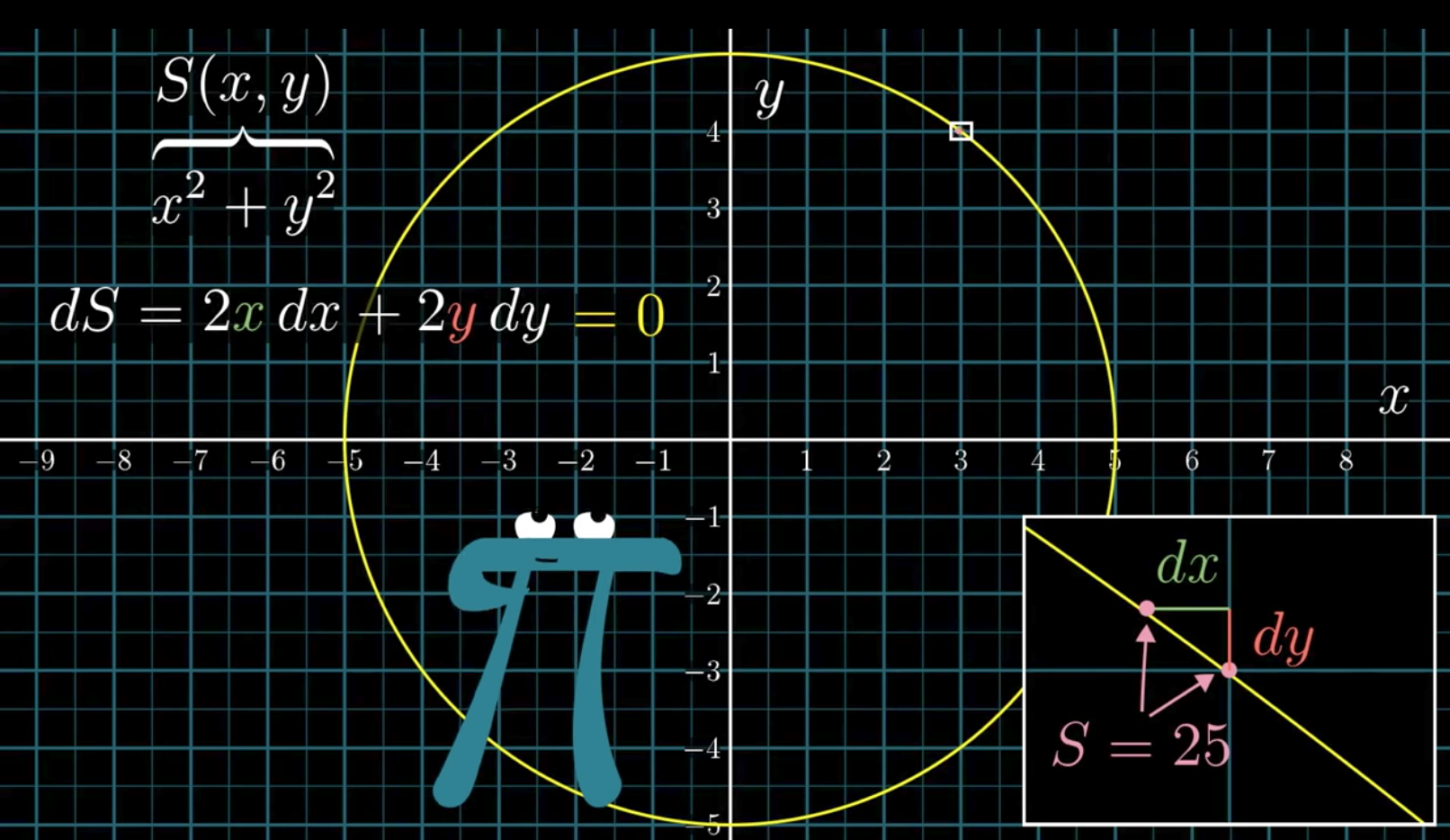
2xdx+2ydy = 0 is the condition under which a tiny step stays on the circle.
Chapter 7
Calculus required continuity, and continuity was supposed to require the infinitely little; but nobody could discover what the infinitely little might be. –Bertrand Russell
The only reason people introduce a new variable name into this formal definition, rather than just using dx, is to be super-extra clear that these changes to the input are ordinary numbers that have nothing to do with the infinitesimal.
The big fuss about limits is that they let us avoid talking about infinitely small changes by asking what happens as the size of some small change to our variable approaches 0.
A limit exists, you can make this output range as small as you want; but when the limit doesn’t exist, that output range can not get smaller than some value, no matter how much you shrink the input range around the limiting input.
Chapter 8
One should never try to prove anything that is not almost obvious. –Alexander Grothendieck
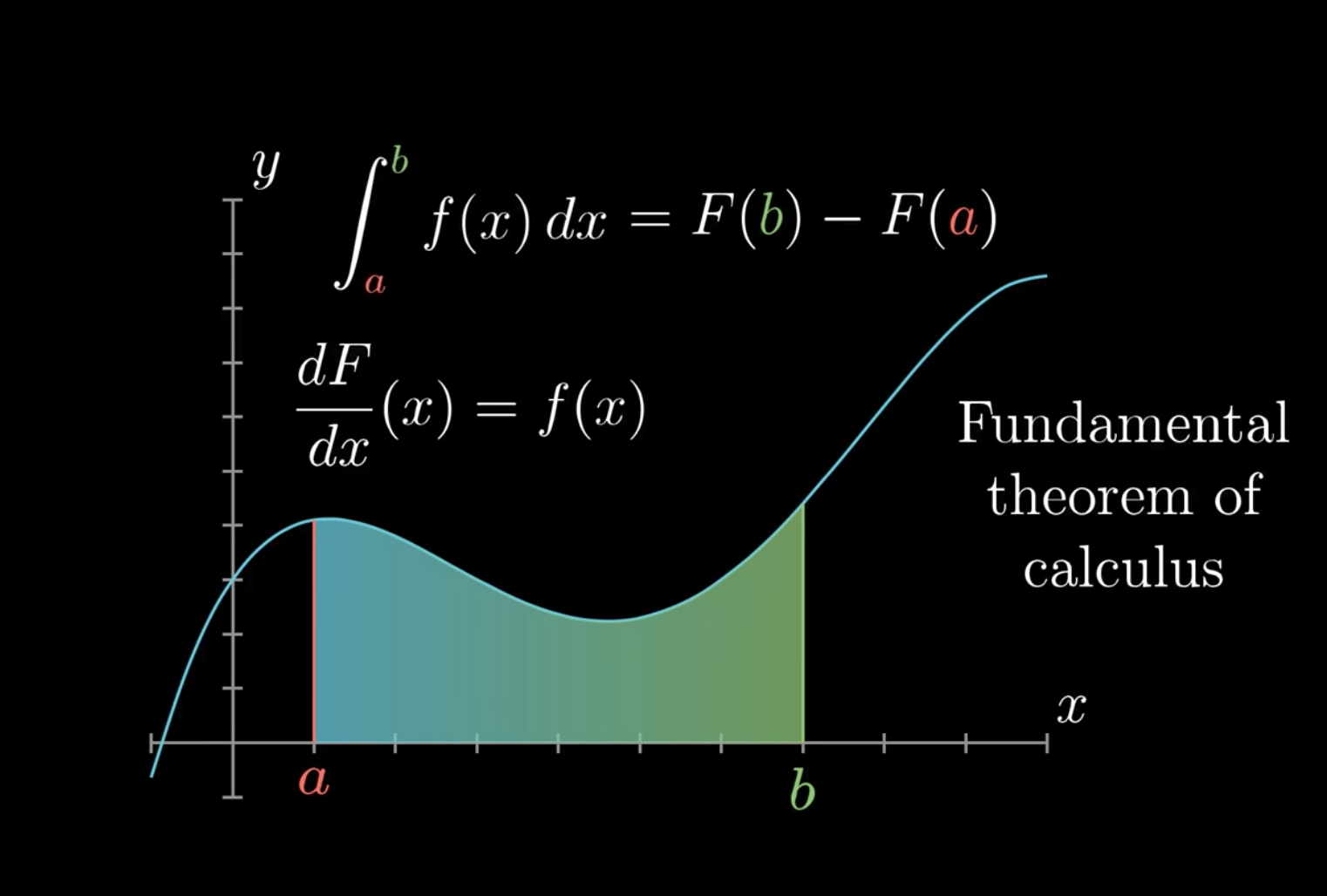
Chapter 9
We often hear that mathematics consists mainly of proving theorems. Is a writer’s job mainly that of writing sentences? –Gian-Carlo Rota
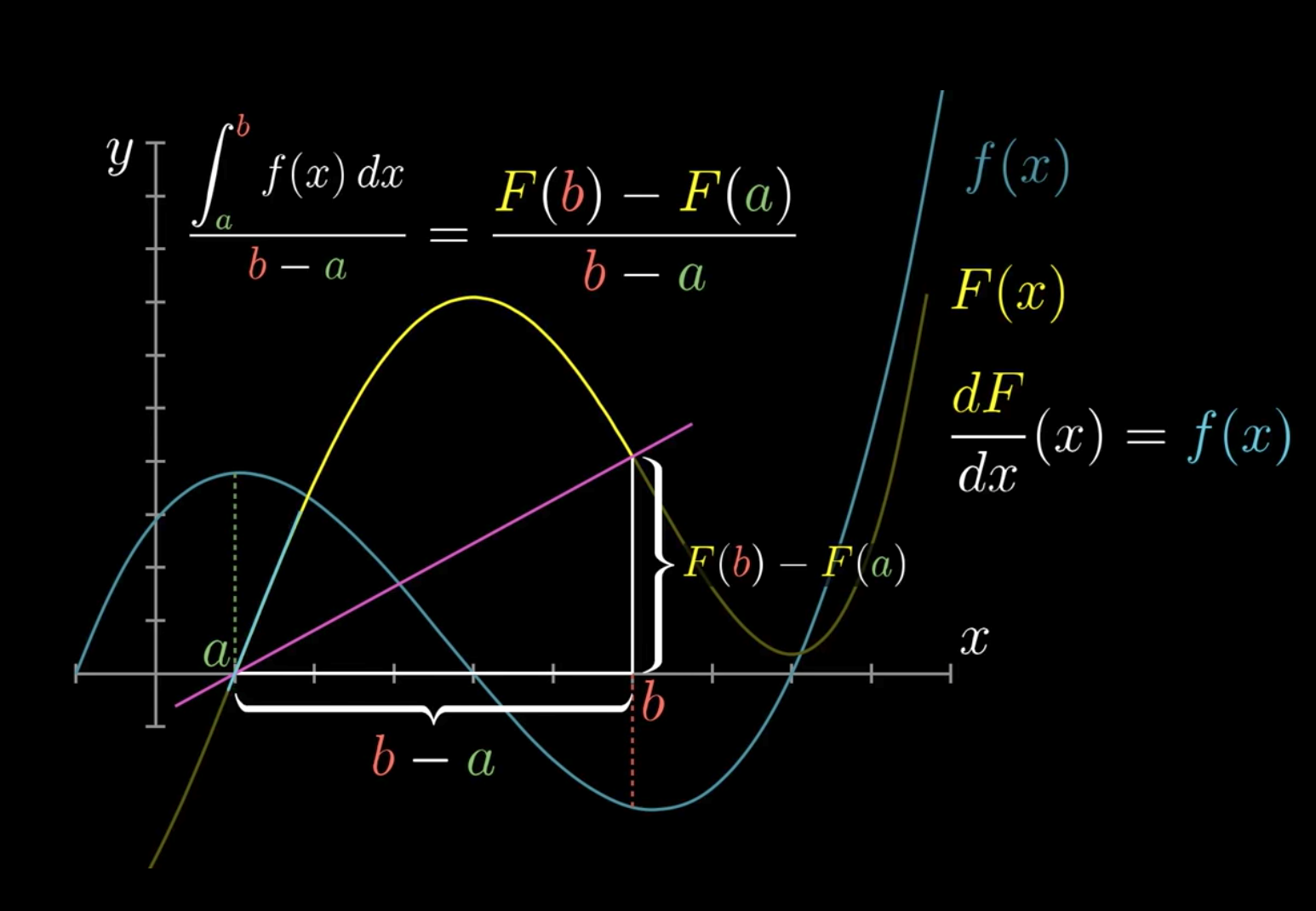
Chapter 10
For me, mathematics is a collection of examples; a theorem is a statement about a collection of examples and the purpose of proving theorems is to classify and explain the examples. –John B. Conway
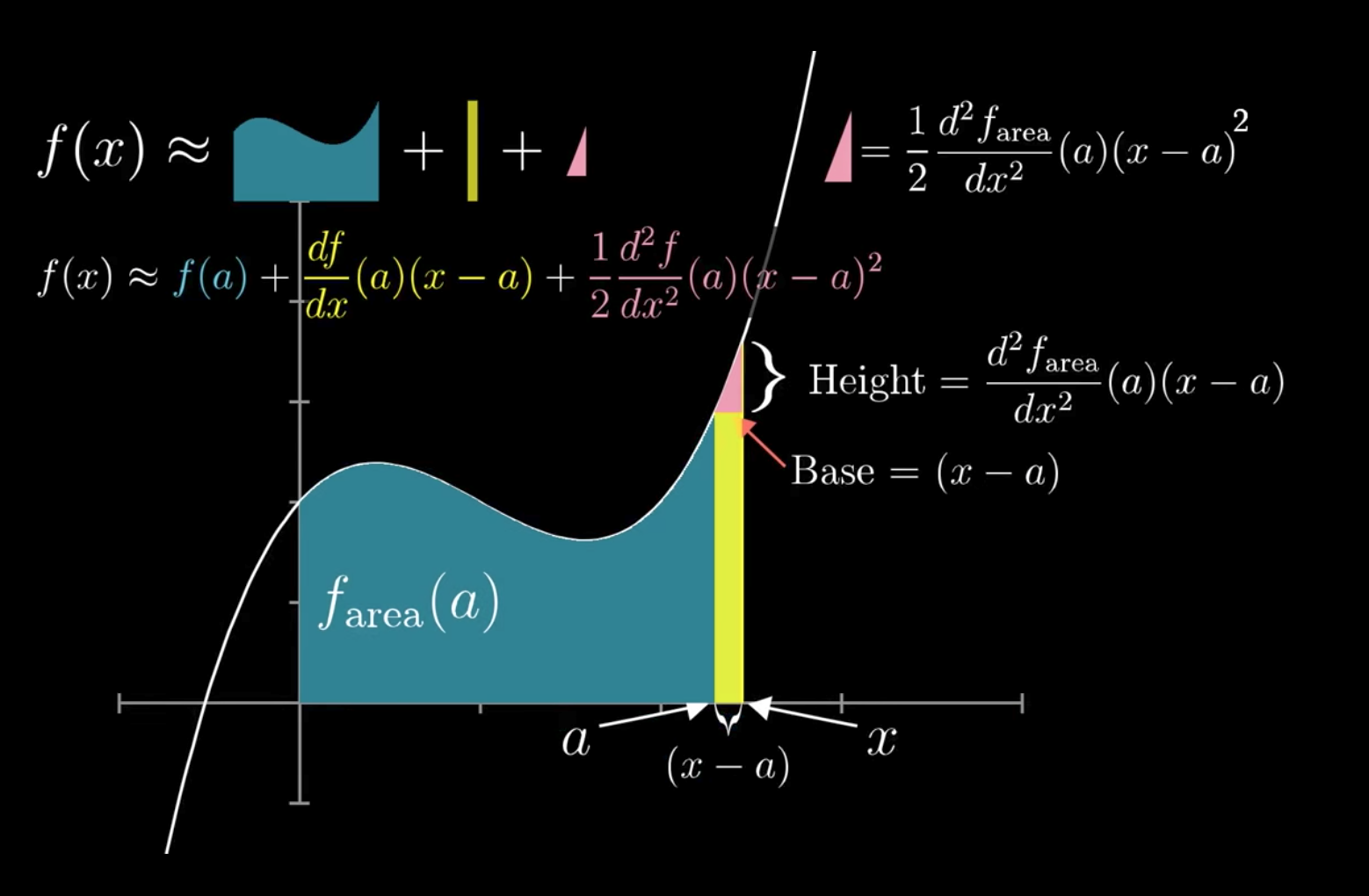
Taylor is one of the most powerful tools that math has to ofer for approximating functions.
Each derivative of a polynomial at x=0 is controlled by one and only one coefficient. Then in order to get the same effect when you were approximating near an non 0 input you would have to write your polynomial in terms of powers of (x - input).
Derivative information at a point -> output information near that point